只要是采用IEEE 754标准的语言都存在这个问题
# JavaScript是如何表示数字的?
JavaScript使用Number类型表示数字(整数和浮点数),遵循IEEE 754标准 通过64位来表示一个数字。表示格式如下:
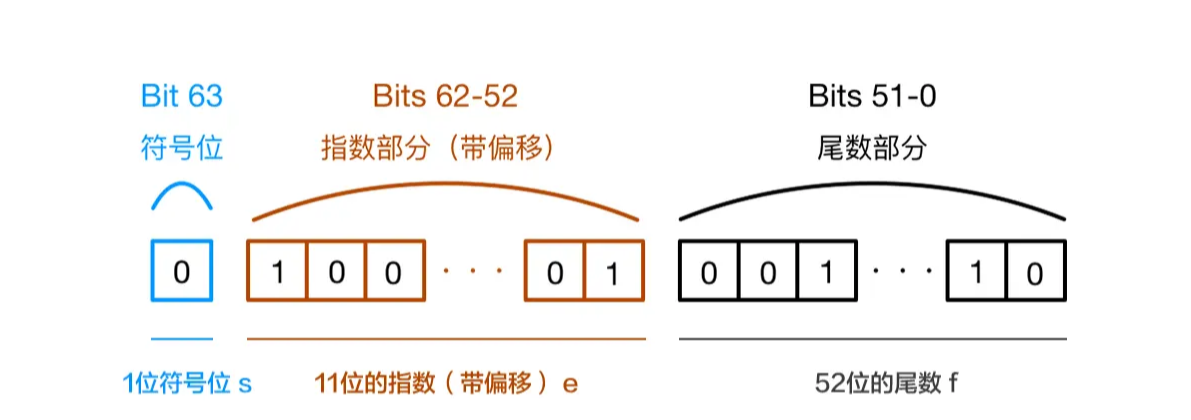
其中
- 第63位是符号位,0表示负1表示正;
- 第52-62位是阶码位,即以2为底的指数部分,计算方式=偏置值(64位字长的偏置值为1023)+求得的阶码真值
- 第0-51位是尾数有效数值位,有效数值位是指小数点后面的数。不管正负,十进制的数都会转换成
1.xxx*2^(阶码真值)的形式
如 100.25 转换成二进制是 1100100.01;规格化后是1.10010001*2^6,其中小数点后面的10010001是尾数有效数值位(后面要填充0直到满足52位数),阶码为111111111+110(即1023+6),因为是正数所以符号位为0。
又有个问题--js最大安全数是Number.MAX_SAFE_INTEGER == Math.pow(2, 53) - 1,而不是Math.pow(2, 52) - 1,尾数部分不是只有52位吗?
如上面🌰所示,十进制的数规格化后都是1.xxx*2^(阶码真值)的形式,所以前面的1可以省略,大家都有的就不必要浪费空间存储了嘛~ 因此,JavaScript提供的有效数字最长为53个二进制位(即64位浮点机器数的后52位+被省略的1位)
# 两个数的运算
计算机无法直接对十进制的数字进行运算,它只认识二进制的数,所以需要先按照IEEE 754转成相应的二进制,然后对阶运算,最后将结果规格化。
0.1 -> 0.0001100110011001...(无限循环)
0.2 -> 0.0011001100110011...(无限循环)
2
由于IEEE 754尾数位数的限制,后面多余的位就会被截掉,所以就会出现精度损失。
# 那为什么赋值 x=0.1 能得到 0.1 呢
53位二进制是js精度范围,它最大可以表示2^53(9007199254740992),转换成的十进制长度为16,所以可以使用toPercision(16)来做精度运算,超过的精度会自动做凑整处理,其中toPercision()的参数可以为1~21,来做不同精度运算。
# 对阶运算
当运算的两个数阶码相等时无需对阶,否则求阶码之差⊿E:
- 如果阶差大于0,则第二个数右移⊿E位,阶码加⊿E
- 如果阶差小于0,则第一个数右移⊿E位,阶码加⊿E
对阶的原则是小阶对大阶,之所以这样做是因为若大阶对小阶,则尾数的数值部分的高位需移出,而小阶对大阶移出的是尾数的数值部分的低位,这样损失的精度更小。对阶后进行尾数加/减。
在进制转换和对接运算中会出现精度损失,造成最后的结果不准确,所以0.1+0.2最后的计算结果转为十进制后就是0.30000000000000004,出现了0.1 + 0.2 != 0.3 的情况。
